Experiments with FIR Digital Filter Design Software
24 Feb 2019 - Jim Evans, G3VDB
Since my early experiments with receiving Radio Teleprinting signals (RTTY) in the 1970s, I have been fascinated by the filtering required. At that time, the design problem was making linear-phase band-pass narrow audio filters built with high-Q toroidal inductors and RC active filters for post-demodulation filters; today the processes for both requirements are purely digital. When you play with Software Defined Radio software such as HPSDR or SDRUno, you can adjust the filtering dynamically by moving the cut-off points on the spectrum. My curiosity was aroused!. How do you design a filter on the fly and apply its design to a signal?
With little understanding of Digital Signal Processing, I tried sources on the Internet. It’s a vast range of related topics. I quickly got lost in this particular convoluted Web. A book was needed to read away from a screen. I settled on Understanding Digital Signal Processing by Richard G. Lyons - Pearson Education.

When the third edition was published, I purchased that too. I am surprised to find that was in September 2012. The expanded edition answered many outstanding questions on filters, modulation and demodulation.
My interest was in writing a multi-channel decoding program that would decode all the active stations in an amateur band, in both RTTY and PSK modes. While I made some progress, designing filters was still obscure. It was clear that the Finite Impulse Response (FIR) filter was ideal for many of my intended purposes. Calculations have no feedback so FIR filters are always stable.
In Chapter 5, Lyons gives two methods of design
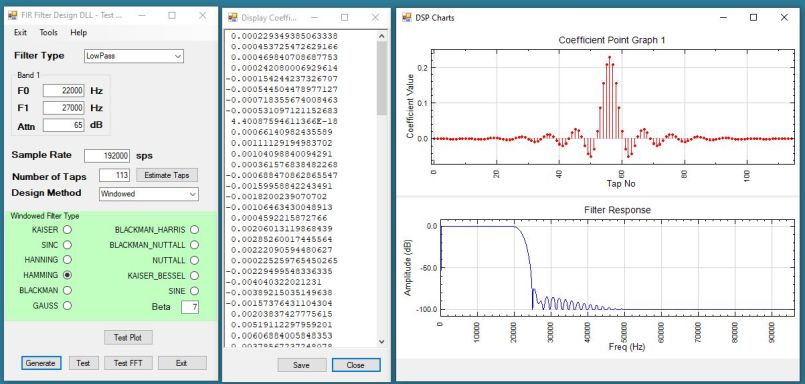
Windowed design was described in some detail; there was no implemenation detail for Parks-McCellan. Dating originally from 1971, Parks-McCellan is described as 'the predominant technique for designing linear-phase FIR filters'. Comparitive responses of filters implemented by the two techniques are shown and Parks-McClellan is clearly superior. That Lyons did not describe the algorithm was a disappointment.
It was time to return to the Internet to find out about this superior algorithm and write some trial code!
I easily found three implementations of Parks-McClellan all in C/C++
- A port to C by Daniel Klostermann of Fortran code found at IowaHills
- A C implementation as used in the OCTAVE open source program under the GNU licence, © (SinCosTbl) 1995,1998 Jake Janovetz janovetz@uiuc.edu.
- A C implementation as distributed with the GNURadio project which is a copy of the OCATAVE code.
If you visit Daniel Klostermann’s site, you will see that his filter design kit is very comprehensive, providing both Windowed and Parks-McClellan functionality (as well as FIR and IIR [Infinite Impulse Response] design).
As I write programs for Microsoft Windows in C#, I translated the C Code of all three implemenations to C#. For speed, I pasted the C code into a Regex design tool RegexBuddy4 and used the search and replace functions to re-write C maths library and functions to the corresponding C# library methods. With a bit of additional manual editing, and, in a much shorter time and with less brain-aching than I had expected, I had code that compiled successfully to a Windows Dynamic Link Library (.dll).
Writing a test-harness Windows Form program to enter parameters to drive the .dll was straight-forward if instructive. But there was more.
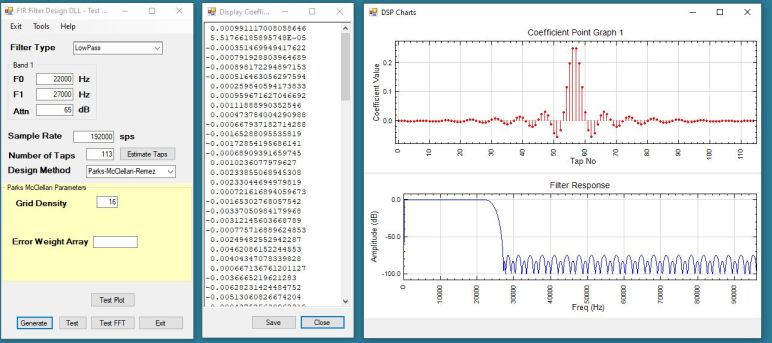
After designing a filter it’s essential (!) to be able to see the expected results. I added the NPlot graphics tool to my program to plot the coefficients. (Plotting the coefficients is equivalent to plotting the Impuise Response of the filter). But what of the all-important Frequency Response?. Here, Digital Signal Processing afficionados can be dismissive. The Frequency Response is easily derived by performing a Fourier Transform on the Impulse Response, or to re-phrase it, by performing a Fourier Transform on the filter coefficients; those design values (numbers) that we just calculated using either Parks-McClellan or the Windowed technique.
I needed a Fourier Transform implementation, or more specifically the computationally-efficient Fast Fourier Transform (FFT). While i am sure many exist, I knew I already had one. Previously, I had produced a C# wrapper for the pskcore.dll by Moe Wheatley, AE4JY to experiment with decoding PSK (and RTTY) signals. The DLL contains an FFT implementation, to produce a spectrum or waterfall. Though written in C++, once again I was able to modify and compile the FFT code C++ code in C#.
So does it work? The following output suggests that it does do something! But of course I have not rigorously compared my design results with other implementations nor with the original FIR suite from Daniel Klostermann. Click on the image for a higher definition version in a new Tab or Window.